1. 스택의 특징
- 선형구조를 갖는다. (자료간의 관계가 1:1이다.)
- 마지막에 삽입한 자료를 가장 먼저 꺼낸다. (LIFO:Last-In-First-Out)
- 자료구조 : 자료를 선형으로 저장할 저장소
- 배열을 사용할 수 있다.
- 스택에서 마지막 삽입된 원소의 위치를 top이라고 부른다. 혹은 stack pointer
cf ) 1차원 배열을 사용하여 구현할 경우, 구현이 용이하지만 스택의 크기를 변경하기 어렵다는 단점이 있다. → 저장소를 동적으로 할당하여 구현하는 방법이 있다. (복잡하지만 메모리를 효율적으로 사용)
스택의 활용 : 괄호검사, function call
2. 재귀호출
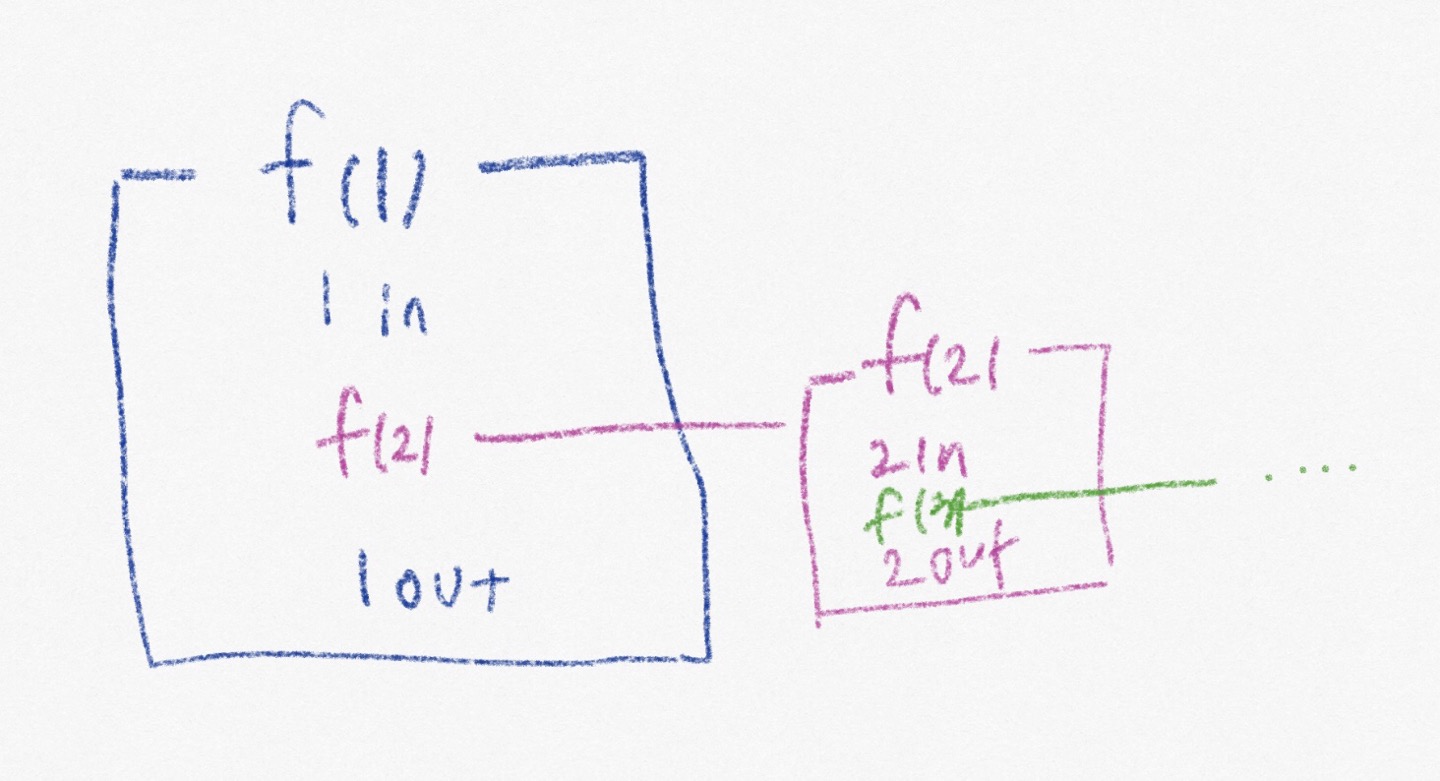
function call을 생각해보자. 예를 들어
def f(n):
if n > 5:
return
else:
print(f"{n} in")
f(n+1)
print(f"{n} out")
f(1)
1 in
2 in
3 in
4 in
5 in
5 out
4 out
3 out
2 out
1 out
함수 안에서 자기 자신을 호출해서 순환 수행을 하고 있다.
일반적인 호출방식보다 프로그램의 크기를 줄이고, 간단하게 작성할 수 있다.
예를 들어 팩토리얼이나 피보나치수열이 유명한 재귀함수이다.
하지만 문제가 있다! 바로 엄청난 중복호출이 발생한다는 것이다!
(출처: 감자일기장)
이렇게 5번째 요소만 호출하는데도 3을 2번, 2를 3번… 이렇게 불필요하게 많이 호출하고 있다! 이말이다.
3. Memoization
메모이제이션은 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 전체적인 실행속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술.
def fibo(n):
if n < 2 :
return n
else :
return fibo(n-1) + fibo(n-2)def fibo1(n):
global memo
if n >=2 and len(memo) <= n:
memo.append(fibo1(n-1) + fibo1(n-2))
return memo[n]
memo = [0,1]n이 작은 수 일때는 별 차이가 없지만, n이 커질수록 실행시간에 큰 차이가 난다.
4. 동적계획 (DP : Dynamic Programming)
위에서 재귀호출과 메모이제이션을 다룬 것은 다 동적계획을 위한 큰 그림이었다!!!
동적계획 알고리즘은 최적화 문제를 해결하는 알고리즘이다. ex ) 그리디 알고리즘
먼저 작은 부분을 해결한 뒤, 그 해들을 이용해서 큰 크기의 문제를 해결하여, 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘이다.
def fibo2(n):
f = [0, 1]
for i in range (2, n+1):
f.append(f[i-1] + f[i-2])
return f[n]위에서 작성한 fibo1은 recursive(재귀) 방식이고, fibo2는 iterative(반복) 방식이다.
- fibo1은 memoization을 사용한다는 점에서는 일반 재귀보다는 실행시간이 적지만, 여전히 재귀적 구조를 사용하기 때문에 스택 오버헤드가 발생할 수 있다.
- DP를 사용해서 구현한 것이 성능 면에서 보다 효율적이다.
Uploaded by N2T