[APS] 8. 트리 (Tree)와 힙 (Heap)

1. 완전 이진트리 (Complete Binary Tree)

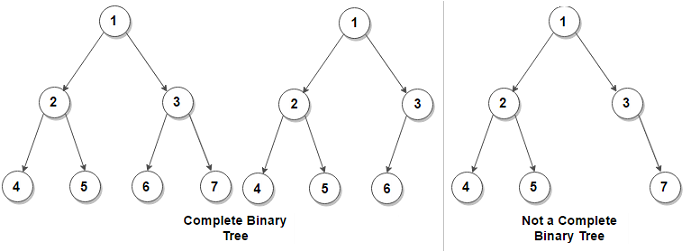
높이가 h이고, 노드 수가 n개 일 때, 포화 이진트리의 노드 번호 1번부터 n번까지 빈자리가 없는 트리

2. 이진 탐색 트리

• 왼쪽 서브트리 < key (루트노드) < 오른쪽 서브트리

• 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리다.

• ‘중위 순회’ 하면 오름차순으로 정렬된 값을 얻을 수 있다.

  def binary(node):
      global k
      # 왼쪽이 비어있으면 왼쪽으로 이동
      if 2*node <=n and nodes[2*node] == 0:
          binary(2*node)
      # 자기 자신을 채우고
      nodes[node] = k
      k = k+1
      # 오른쪽으로 이동한다.
      if 2*node+1 <=n and nodes[2*node + 1] == 0:
          binary(2*node+ 1)
  
  T = int(input())
  for tc in range(1, T+1):
      k = 1
      n = int(input())
      # 이진 탐색 트리는 중위 순회의 역순으로 넣으면 된다.
      nodes = [0 for _ in range(n+1)]
      binary(1)
      print(f"#{tc} {nodes[1]} {nodes[n//2]}")

3. 힙(heap)

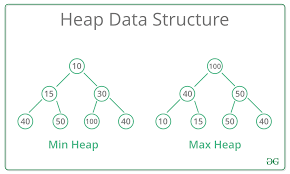
• 최대 힙(max heap)
  • 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
  • 부모 노드의 키 값 > 자식 노드의 키 값
  • 루트 노드 : 키 값이 가장 큰 노드

• 최소 힙(min heap)
  • 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
  • 부모 노드의 키 값 < 자식 노드의 키 값
  • 루트 노드 : 키 값이 가장 작은 노드

• 힙 연산에서의 삽입(enque)

  # index 번호(last)를 하나 추가한다.
  # heap[last] = n
  # 이후에 부모와 비교해서 자리를 재배치 한다.
  # 자식 = 들어온 노드
  # 부모 = 자식 //2
  
  # 부모가 존재하고, 자식이 부모보다 크다면 (while)
  	# 자리를 변경한다.
  	# 또 다시 변경해야 할 수 있으므로, p,c를 갱신한다.

• 힙 연산에서의 삭제(deque) → 루트 노드만 삭제할 수 있다.

  # 현재의 1번값을 저장해 둔다.
  # 루트 노드에 맨 마지막(last)의 값을 옮기고,
  # last를 삭제한다.
  
  # 부모 = 1, 자식 = 부모 //2
  # 자식이 있는 경우, 비교를 시작한다. (while)
  	# 오른쪽 자식도 있고, 왼쪽 자식 < 오른쪽 자식이면 비교대상을 오른쪽으로 한다.
  	# 자식 > 부모이면,
  		# 자리를 변경하고 갱신한다.
  	# 그렇지 않다면, 반복문을 중단한다.

Uploaded by N2T